Numerisches Integrieren
Es wird hier das bestimmte Integral für eine Funktion f(x) im Bereich x1≤x≤x2 numerisch berechnet.
Parallel können verschiedene numerische Methoden verwendet werden: Trapez-Regel, Simpson-Regel, Gauß-Quadratur-Verfahren sowie Integration nach Fejér.
Voraussetzung ist, dass der angegebene Funktionsverlauf im Bereich x1<x<x2 definiert ist und keine Polstellen hat.
Die Schrittweite der numerischen Integration ist h. Das Intervall [x1,x2] wird für die Integration in gleichlange Bereiche ungefähr dieser Größe h unterteilt.
Schrittweite und Stützstellen der numerischen Integration
Für die Simpsonregel wird eine ungerade Anzahl von Stützstellen benötigt.
Die angegebene Schrittweite wird deshalb ggf. geringfügig verkleinert.
Zu beachten ist ferner, dass die Gauß-Integration pro Intervall 2 bzw. 3 Funktionsauswertungen benötigt.
Die Mittelpunktsregel benötigt pro Intervall eine Funktionsauswertung und
die anderen Methoden benötigen je eine Funktionsauswertung an den Intervallgrenzen.
Die Mittelpunktsregel und die Gauß-Verfahren benötigen keine Auswertung an den Rändern des Gebiets.
Das ist von Vorteil, wenn der Integrand am Rande das Gebietes eine hebbare Definitionslücke hat wie z.B. x·ln(x) bei x=0.
Auch konvergente uneigentliche Integrale 1. Art, wie das Integral über ln(x) von 0 bis 1, sind für diese Verfahren kein Problem.
Erläuterung zur grafischen Darstellung
Das bestimmte Integral für eine Funktion f(x) liefert die gewichtete Summe der Flächenanteile, die die Funktion f(x) im Bereich [a,b] mit der x-Achse einschließt.
Dabei werden Flächenanteile, die unterhalb der x-Achse liegen, mit negativem Vorzeichen, d.h. mit -1 gewichtet, in die Summe eingebracht.
Das bestimmte Integral ergibt dann die Differenz der Summe der Flächenanteile die oberhalb der x-Achse liegen und derer die unterhalb der x-Achse liegen.
Die grafische Darstellung macht zwischen den positiven und negativen Summanden der Berechnung keinen Unterschied.
Fläche zwischen 2 Kurven
Manchmal soll der Flächeninhalt einer Fläche bestimmt werden, die von 2 Kurven für ein Intervall [a,b] der x-Achse eingeschlossen wird.
Sind die Kurven als Funktionen f(x) und g(x) gegeben, dann liefert das bestimmte Integral von |f(x)-g(x)| den eingeschlossenen Flächeninhalt.
Das gilt auch dann, wenn sich die beiden Kurven im Intervall [a,b] schneiden.
Die Fläche zwischen der Kurve von f(x) und der x-Achse g(x)=0 ist demnach berechenbar über das bestimmte Integral von |f(x)|.
Sehnentrapezregel, Mittelpunktsregel und Simpsonregel
Für die einfachsten numerischen Konzepte werden hier die zugrunde liegenden Formeln angegeben.
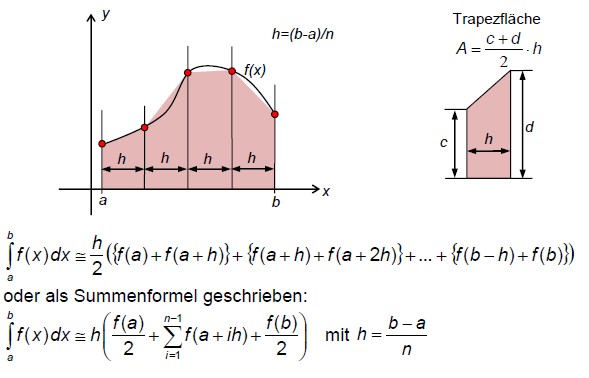
Sehnentrapezregel
Bei der Sehnentrapezregel (bzw. kurz Trapezregel) wird das Integral für ein Intervall durch eine Trapezfläche angenähert.
Das Trapez wird dabei durch die Sehne an die Funktion im jeweiligen Intervall festgelegt.
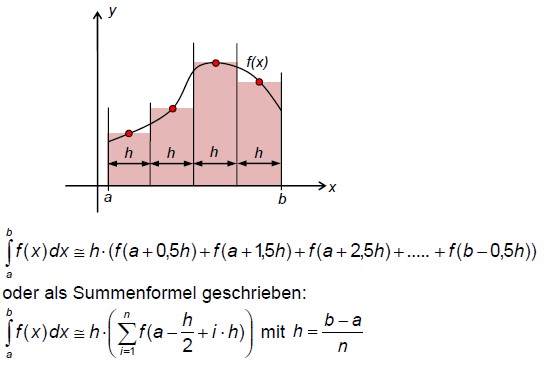
Mittelpunktsregel
Die Mittelpunktsregel ist im Prinzip das Gleiche wie die Tangenten-Trapezregel.
Man kann nämlich die horizontale Gerade einer jeden Rechteck-Flächenbegrenzung um ihren (hier roten) Mittelpunkt
so drehen, dass sie dort zur Tangente an die Kurve von f(x) wird, ohne dass sich die eingeschlossene Trapezfläche ändert.
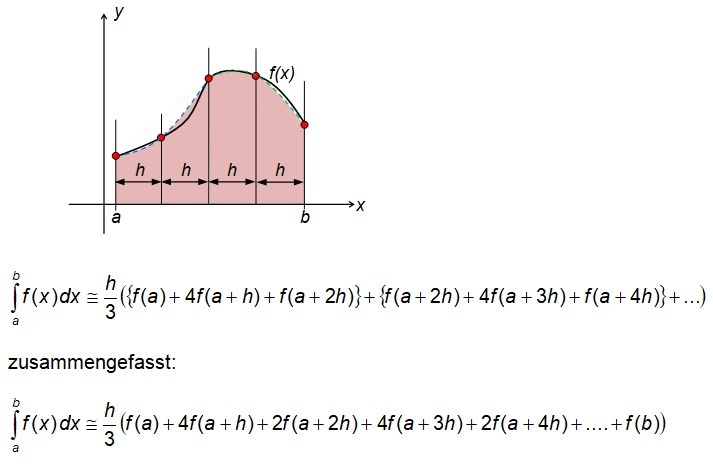
Simpsonregel
Die Simpsonregel benötigt eine gerade Anzahl von Streifen bzw. eine ungerade Anzahl von Stützpunkten.
Für je 3 benachbarte Stützpunkte wird die Funktion f(x) dann durch eine interpolierende Parabel ersetzt und deren Verlauf integriert.
weitere JavaScript-Programme


