Integrales Definidas
Aquí la integral definida para una función f(x) en el intervalo [x1,x2] se puede calcular numéricamente.
Se pueden utilizar varios métodos numéricos en paralelo: regla trapezoidal, de Simpson y de Fejér, así como métodos de cuadratura gaussiana.
El requisito previo es que la curva de función especificada esté definida en el área x1<x<x2 y no tenga singularidades allí.
El tamaño del paso de la integración numérica es h. Para la integración, el intervalo [x1,x2] se divide en áreas de igual longitud de aproximadamente este tamaño h.
Tamaño del paso de la integración
La regla de Simpson requiere un número impar de puntos de apoyo.
Por lo tanto, el tamaño del paso especificado puede reducirse ligeramente.
También cabe señalar que la integración gaussiana requiere 2 o 3 evaluaciones de funciones por intervalo.
La regla del punto medio requiere una evaluación de función por intervalo y
los otros métodos requieren cada uno una evaluación de función en los límites del intervalo.
La regla del centro y los métodos gaussianos no requieren evaluación en los bordes del área.
Esto es una ventaja si el integrando en el borde del dominio tiene un espacio definible en la definición, como x*ln(x) en x=0.
Incluso las integrales impropias convergentes del primer tipo, como la integral sobre ln(x) de 0 a 1, no son un problema para estos métodos.
Explicación de la representación gráfica
La integral definida para una función f(x) devuelve la suma ponderada de los componentes del área que la función f(x) encierra en el área [a,b] con el eje x.
Las partes del área que se encuentran debajo del eje x se incluyen en el total con un signo negativo, es decir, ponderadas con -1.
La integral definida entonces resulta en la diferencia de la suma de las porciones de área que se encuentran sobre el eje x y las que se encuentran debajo del eje x.
La representación gráfica no distingue entre las sumas positivas y negativas del cálculo.
Área entre 2 curvas
A veces se desea determinar el área de una superficie encerrada por 2 curvas para un intervalo [a,b] del eje x.
Si las curvas se dan como funciones f(x) y g(x), entonces la integral definida de |f(x)-g(x)| da el área cerrada.
Esto también se aplica si las dos curvas se cruzan en el intervalo [a,b].
Por lo tanto, el área entre la curva de f(x) y el eje x g(x)=0 se puede calcular usando la integral definida de |f(x)|.
Regla del trapecio, regla del punto medio y regla de Simson
Aquí se proporcionan las fórmulas subyacentes para los tres conceptos numéricos más simples.
Regla del trapecio
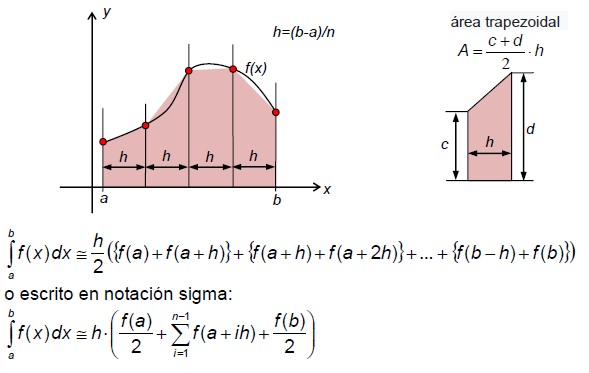
Regla del punto medio
La regla del punto medio es básicamente la misma que la regla del trapecio tangente.
Puedes rotar la línea horizontal de cualquier límite del área del rectángulo alrededor de su centro hasta que se vuelva tangente a la curva de f(x) sin cambiar el área trapezoidal cerrada.
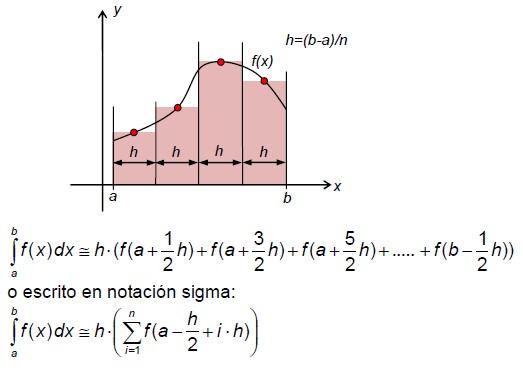
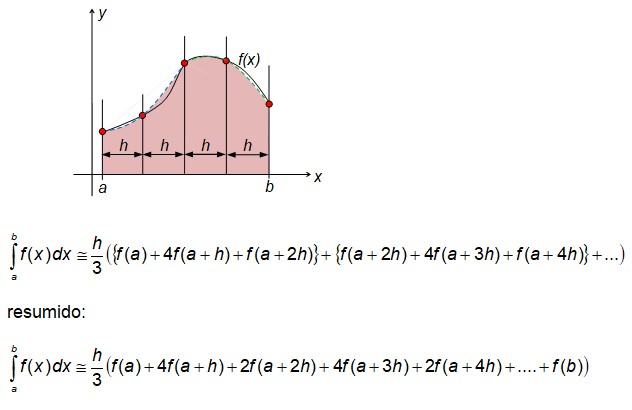
Regla de Simpson
La regla de Simpson requiere un número par de tiras o un número impar de puntos de apoyo.
Por cada tres puntos de apoyo adyacentes, la función f(x) se sustituye por una parábola interpoladora y su forma se integra.
otras aplicaciones en JavaScript


