2D-Tragwerk berechnen mit FEM
Berechnet werden Schnittgrößen (Biegemoment, Querkraft, Normalkraft), Lagerreaktionen und der Verschiebungszustand für ebene, auch statisch unbestimmte Balken und Tragwerke.
Dazu wird die Methode der finiten Elemente (FEM) angewendet.
Zu den Modelldaten
Ein zu untersuchendes Modell wird festgelegt durch:
- Sämtliche Punkte, an denen das Tragwerk gelagert ist, wo Lasten eingeleitet werden und wo Querschnittsprünge vorliegen.
Bei der Eingabe der Punkt-Koordinaten kann man auf die Koordinaten anderer Punkte über x1,y1,x2,y2 usw. zugreifen.
Ferner kann man die Knotenpunkte durch Klickziehen mit der Maus verschieben.
- Eine Liste der Elemente des Tragwerks. Für jedes Element müssen seine 2 Endpunke angegeben werden.
Ferner wird sein Materialindex benötigt (z.B. 1, wenn man nur ein Material verwendet).
Der letzte Eintrag (Typ) legt fest, ob es ein Balken (Typ 0), ein Fachwerkstab (Typ 3) oder ein Balken mit Gelenk vorn (Typ 1) oder hinten (Typ 2) ist.
Man kann Elemente auch mit der Maus durch Klickziehen anlegen.
- Angaben zum Material. Das sind hier Querschnittsfläche A, Flächenträgheitsmoment I und E-Modul.
- Angaben zur Belastung. Hier kann die Belastung der jeweiligen Knoten angegeben werden.
- Angaben zur Lagerung. Hier kann punktbezogen sowohl in x- als auch in y-Richtung sowie gegen Drehbewegung gefesselt werden.
Das Programm ist eigentlich primär für die Untersuchung von Rahmentragwerken konzipiert.
Rahmentragwerke bestehen normalerweise nur aus Balkenelementen vom "Typ 0", die biegesteif untereinander verbunden sind.
Man kann aber mit Hilfe von "Typ 3" bei den Elementen auch Fachwerkstäbe verwenden.
Ferner kann man mit Hilfe "Typ 4" bei den Elementen Federn verwenden.
Bei Federn muss ein "Material" verwendet werden, wo anstelle des Elastizitätsmoduls die entsprechende Federsteifigkeit steht.
Ferner müssen die Querschnittsfläche A und das Flächenträgheitsmoment I auf 0 gesetzt werden.
Bei der Dateneingabe existieren keine Einheiten. Der Benutzer ist selber dafür verantwortlich Daten bezüglich verträglicher Einheiten bereitzustellen,
z.B. Punkt-Koordinaten in m, Lasten in N, Querschnitte in m² und den E-Modul in N/m². Verschiebungen entstehen dann in m, Stabkräfte in N.
Zu den Ergebnissen
Die Vorzeichen der ausgegebenen Verschiebungen und Lagerreaktionen beziehen sich auch ein globales xy-Koordinatensystem, das standardmäßig ausgerichtet ist.
Die Darstellung der Verschiebungen (Biegelinie) verwendet einen Vergrößerungsfaktor, der so gewählt ist, dass Verschiebungen überhaupt sichtbar werden.
Als Schnittgrößen werden für Balkenelemente die Normalkraft N, die Querkraft Q und das Biegemoment M bestimmt und ausgegeben.
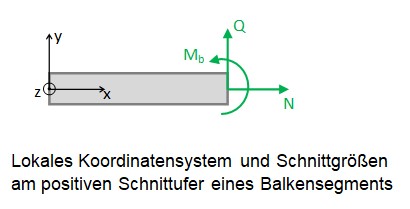
Zusätzlich zur tabellarischen Ausgabe der Schnittgrößen kann man die einzelnen Elemente auch anklicken und erhält dann die zugehörigen Schnittgrößen angezeigt.
Da die Normalkraft und die Querkraft konstant in jedem Element sind (das Programm kennt keine Streckenlasten), wird pro Element nur ein Wert angegeben.
Anders ist das beim Biegemoment. Es verändert sich im Allgemeinen linear von Knoten zu Knoten, so dass hier 2 Werte ausgegeben werden.
Um sie richtig zuordnen zu können, sind sie mit der globalen Knotennummer indiziert.
Für Stabelelemente sind die Querkraft und das Biegemoment stets 0.
Deshalb wird bei Stabelementen auf die Ausgabe dieser Schnittgrößen verzichtet.
weitere JavaScript-Programme