Tragwerks- und Balkenschwingungen
Es werden hier Eigenschwingungen von ebenen Balkenstrukturen und Rahmentragwerken untersucht.
Berechnet werden Eigenfrequenzen und Eigenformen. Die Schwingungen der Strukturen in den Eigenformen werden simuliert.
Zu den Modelldaten
Ein zu untersuchendes Modell wird festgelegt durch:
- Sämtliche Punkte, an denen das Tragwerk gelagert ist, wo lokale Massen sitzen oder wo Querschnittssprünge vorliegen.
Bei der Eingabe der Punkt-Koordinaten kann man auf die Koordinaten anderer Punkte über x1,y1,x2,y2 usw. zugreifen.
Ferner kann man Knotenpunkte durch Doppelklick anlegen und durch Klickziehen mit der Maus verschieben.
- Eine Liste der Elemente des Tragwerks. Für jedes Element müssen seine 2 Endpunke angegeben werden.
Ferner wird sein Materialindex benötigt (z.B. 1, wenn man nur ein Material verwendet).
Der letzte Eintrag (Typ) legt fest, ob es ein Balken (Typ 0), ein Fachwerkstab (Typ 3) oder ein Balken mit Gelenk vorn (Typ 1) oder hinten (Typ 2) ist.
Man kann Elemente auch mit der Maus durch Klickziehen anlegen.
- Angaben zum Material. Das sind hier Querschnittsfläche A, Flächenträgheitsmoment I, E-Modul und Materialdichte ρ.
- Angaben zu lokalen Massen - falls vorhanden.
Wird nur der Parameter m angegeben, sind es Punktmassen (2 Freiheitsgrade).
Wird auch der Parameter J angegeben, so wird dieses Masseträgheitsmoment berücksichtigt (3 Freiheitsgrade).
- Angaben zur Lagerung. Hier kann punktbezogen sowohl in x- als auch in y-Richtung sowie gegen Drehbewegung gefesselt werden.
Rahmentragwerke können hier mit Balkenelementen mit und ohne Massenträgheit modelliert werden, je nachdem, ob man eine Dichte ρ angibt oder nicht.
Verwendet man nur Balkenelemente ohne Eigenmasse, muss das System irgendwo mindestens eine lokale schwingfähige Masse haben.
Werden Balkenelemente ohne Eigenmasse verwendet, ist eine feine Unterteilung der Struktur mit Elementen nicht nötig.
Anders im Falle von Balkenelementen mit Eigenmasse. Hier ist es so, dass man dann mit mehr Elementen mehr Eigenfrequenzen errechnen kann.
Weil das Programm keine Einheiten kennt, ist der Benutzter selbst verantwortlich dafür,
dass die Eingabedaten konsistent sind. Am einfachsten verwendet man von daher Daten im SI-Einheiten-System.
D.h. Koordinaten in m, Kräfte in N, Massen in kg, Massenträgheitsmomente in kgm², usw.
Ursprünglich sollte das Programm nur Balkenelemente (Biegefedern) und Fachwerkstäbe verarbeiten können.
Als kleine (nicht ganz gelungene) Erweiterung kann man aber auch normale Federn verwenden.
Die sind der "Typ 4". Federsteifigkeit und (optional) Masse werden über die Materialeigenschaft Ei und ρi bereitgestellt.
Federn haben im Prinzip die gleiche Steifigkeitsmatrix wie Fachwerkstäbe, nur dass ihre Steifigkeit direkt gegeben ist und sich nicht aus A·E/L errechnet.
Zu den Ergebnissen
Wird das Kontinuum des Balkens mit FEM modelliert, so sind die errechneten Eigenfrequenzen stets nur Näherungen für die exakten Eigenfrequenzen des Kontinuums.
Für die errechneten Eigenfrequenzen wird die Näherung mit steigender Eigenfrequenz immer schlechter.
Grund dafür ist, dass mit steigender Eigenfrequenz der Biegeneigenschwingungen eines Balkens die zugehörigen Eigenformen immer mehr Schwingungsknoten (Nulldurchgänge) haben.
Damit steigt automatisch auch die Anzahl der Wendepunkte bzw. Krümmungswechsel entlang der jeweiligen Eigenform.
Die für die finiten Elemente verwendeten Ansatzfunktionen sind hier Polynome 3. Grades.
Diese Polynome können solche Krümmungswechsel sinusähnlicher Verläufe kürzer werdender Wellenlänge immer schlechter annähern.
Je feiner man dann mit Elementen modelliert, umso besser werden deshalb die Näherungen auch für höhere Eigenfrequenzen.
Bei den Eigenformen werden für jeden Knoten 2 Verschiebungen (u und v) und eine lokale Verdrehung (β) ausgegeben.
Die Verdrehunug ist ein Winkel in Radian.
Die Eigenformen sind so skaliert, dass der größte Wert im Eigenvektor 1 ist.
Das macht natürlich insbesondere für die Winkel, wenn man sie in Grad umrechnen will, anschaulich keinen Sinn,
ist aber Folge der linearen Berechnung, die ja die Bestimmung der Eigenvektoren nur bis auf einen beliebigen Faktor ermöglicht.
Sollte das untersuchte Modell nicht mindestens statisch bestimmt gelagert und damit kräftefreie Verschiebungen bzw. Verdrehungen möglich sein,
so existieren stets auch Eigenfrequenzen 0. Die zugehörigen Eigenformen beschreiben jeweils die Bewegungen, die kräftefreie möglich sind.
Exemplarischer Vergleich mit theoretischen Ergebnissen
In der Regel lassen sich die Eigenfrequenzen von Strukturen aus Biegebalken nicht exakt analytisch bestimmen.
Anders ist das beim Sonderfall des Biegebalkens mit gleichförmigem Querschnitt.
Für den lassen sich für unterschiedliche Lagerungen der beiden Enden analytisch die Eigenfrequenzen bestimmen.
So sind für den Fall beidseitig gelenkiger Lagerung an den Enden die Eigenkreisfrequenzen der Biegeschwingungen:
ωk = (k·π/L)2 (E I)1/2/(ρ A)1/2.
Somit folgt für die Eigenfrequenzen fk:
fk = k2 π/2 (E I)1/2/(ρ A L4)1/2
Der Zahlenfaktor k2 π/2 vor dem Einheiten behafteten Bruch liefert die Eigenfrequenzen für den Sonderfall E=I=A=L=ρ=1.
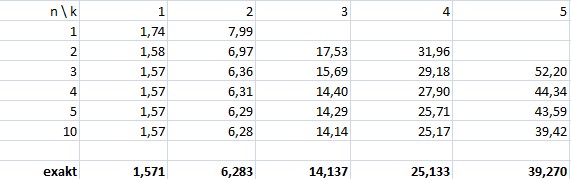
Für diese Parameterkonstellation wurden die Näherungslösungen für Modelle mit unterschiedlicher Anzahl (n) von Elementen bestimmt.
Die abgebildete Tabelle stellt die Näherungslösungen fk(n) den exakten Werten gegenüber.
Für den Fall beidseitig gelenkiger Lagerung an den Enden sind die Eigenkreisfrequenzen der Longitudinalschwingungen:
ωk = k·π/L (E/ρ)1/2.
Es folgt für die Eigenfrequenzen fk:
fk = k/2 (E/ρ)1/2/L.
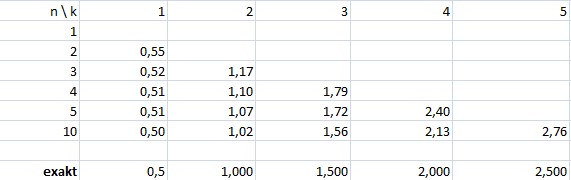
Für die Parameterkonstrellation E=L=ρ=1 stellt die folgend abgebildete Tabelle die Näherungslösungen fk(n) für Modelle mit unterschiedlicher Anzahl von Elementen (n) den exakten Werten gegenüber.
Modale Daten
Das Bewegungsdifferentialgleichungssystem eines ungedämpften Mehrmassenschwingers ist gegeben durch
M u•• + K u = 0.
Wenn man die Eigenvektoren φi des zugehörigen Systems
(-ω2M + K) φ = 0
bestimmt und spaltenweise zu einer Matrix Φ zusammenstellt, kann man das Differentialgleichungssystem in eines überführen,
bei dem die Gleichungen entkoppelt sind:
ΦTM Φ v•• + ΦTK Φ v = 0.
In v stehen jetzt die neuen generalisierten Koordinaten des Systems.
Auf der Haupdiagonale der neuen Massenmatrix ΦTM Φ stehen dann die sogenannten generalisierten Massen.
Auf der Haupdiagonale der neuen Steifigkeitsmatrix ΦTK Φ stehen dann die sogenannten generalisierten Steifigkeiten.
Die beiden Matrizen sind Diagonalmatrizen, sind also außerhalb der Diagonale mit 0 belegt.
weitere JavaScript-Programme

