Shear Force and Bending Moment in Beams and Frames
For statically determinate beams and frames support reactions, bending moment, shear force and axial force are calculated and visualized in diagrams.
Steps to set up a new model
- define coordinates of all relevant points (bearing and load locations).
The mouse can be used: double click to create new points, click drag to move existing points
- define for points with bearings, which direction is supported
- define loads
General observations
With straight beams, the curves of the 3 internal forces are continuous except at the points where the associated loads/support reactions act.
At such load application points, there are jumps in the size of the applied load.
Assuming only point loads exist, the following applies:
- The course of the normal force and the course of the shear force are constant beyond the jump points due to the introduction of loads.
- The bending moment curve generally changes linearly, but can also be constant.
In the case of differently aligned substructures, the shear force curve and the normal force curve show jumps at the vertices of the structure.
However, the course of moments at the vertices is usually continuous.
Moment jumps only occur when a moment acts on a vertex.
Regarding loads
The program only knows point loads.
For a structure under a constant line load q0 you can get an approximate solution:
You need to create several equidistant points in the loaded area of length L.
With n points (n including the start and end point), each inner point receives a point load of q0L/(n-1) and the two edge points each receive half of that.
To the results
Only if a horizontal bar is examined, the respective internal force is plotted in the diagram as an ordinate.
The signs of the internal forces are based on a local xyz coordinate system,
whose x-axis points in the structure direction and whose z-axis points to the right of that.
The y-axis points out of the display plane towards the viewer.
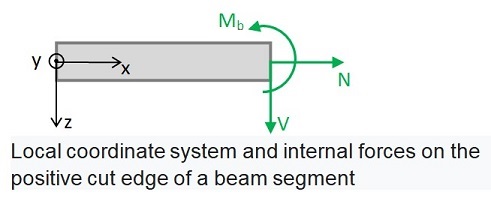
A bending moment at the right end of a beam segment (positive cut bank) is positive,
if it acts to the right around the y-axis pointing out of the representation plane.
A shear force is positive at the right end of a beam segment if it acts to the right of the structure.
In frame constructions, the signs are also based on the local xyz coordinate system of the respective substructure with coordinate origin in its first node.
These coordinate systems will of course be aligned differently in space for the substructures.
Longitudinal forces are easiest to discuss in terms of signs:
Positive normal forces represent a tensile load, negative normal forces represent a compressive load.
The program does not know any line loads.
Constant line loads can, however, be represented relatively well by a group of individual loads (see above).
The associated moment curve is then a polygon.
At the corners of the polygon the results agree with the exact results,
which are given by a square course in the range of the line load.
The associated shear force course is then step-shaped (discontinuous).
In the middle of each step interval will be agreement with the continuous exact course.
more JavaScript applications
