Diagramas de Fuerza Cortante y Momento Flexionante
Para vigas y estructuras determinadas estáticamente, se calcula reacciones de apoyo, momento flexionante, fuerza cortante y fuerza axial.
Se muestran los diagramas asociados de las fuerzas internas.
Pasos para configurar un nuevo modelo
- definir las coordenadas de todos los puntos relevantes (puntos de carga y puntos de apoyo).
Se puede usar el ratón: haga doble clic para crear nuevos puntos, haga clic y arrastre para mover puntos existentes.
- definir para puntos con apoyo, qué dirección es suportado
- definir cargas
Observaciones generales
Con vigas rectas, las curvas de las 3 fuerzas internas son continuas excepto en los puntos donde actúan las cargas/reacciones de apoyo asociadas.
En tales puntos de aplicación de carga, hay saltos del tamaño de la carga aplicada.
El curso de la fuerza normal y el curso de la fuerza cortante son constantes más allá de los puntos de salto debido a la introducción de cargas.
En estas áreas, la curva del momento flector es linealmente variable.
En el caso de estructuras con subáreas alineadas de manera diferente, la curva de fuerza cortante y la curva de fuerza normal tienen saltos en las vertices de la estructura.
Sin embargo, la progresión de momentos en las vertices suele ser continua.
Los saltos solo ocurren cuando actúa un momento en un vértice.
Cómo hacer frente a las cargas distribuidas
El programa solo conoce cargas puntuales.
Para una estructura bajo una carga distribuida constante q0, puede obtener una solución aproximada:
Necesita crear un grupo de puntos equidistantes en el área cargada de longitud L.
Con n puntos (n incluyendo el punto inicial y final), cada punto interior recibe una carga puntual de q0·L/(n-1) y los dos puntos del borde reciben cada uno la mitad de eso.
A los resultados
Sólo si se examina una barra horizontal, la fuerza interna respectiva se representa en el diagrama en forma de ordenadas.
Los signos de las fuerzas internas se basan en un sistema de coordenadas local xyz,
cuyo eje x apunta en la dirección de la estructura y cuyo eje z apunta a la derecha de esa.
El eje y apunta fuera del plano de visualización hacia el espectador.
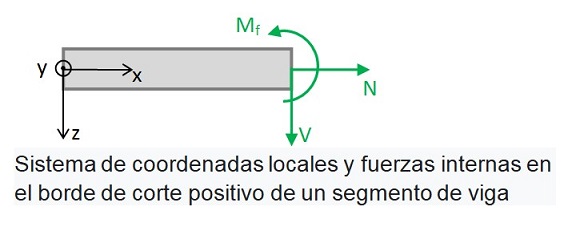
Un momento flector en el extremo derecho de un segmento de viga (banco de corte positivo) es positivo,
si actúa hacia la derecha alrededor del eje y apuntando hacia afuera del plano de representación.
Una fuerza cortante es positiva en el extremo derecho de un segmento de viga si actúa hacia la derecha de la estructura.
En las construcciones de marcos, las señales también se basan en el sistema de coordenadas local xyz de la respectiva estructuras parciales con origen de coordenadas en su primer nodo.
Naturalmente, estos sistemas de coordenadas se alinearán de forma diferente en el espacio para las estructuras parciales.
Las fuerzas longitudinales son más fáciles de analizar en términos de signos:
Las fuerzas normales positivas representan una carga de tracción, las fuerzas normales negativas representan una carga de compresión.
El programa no conoce ninguna carga de línea.
Sin embargo, las cargas lineales constantes pueden representarse relativamente bien mediante un grupo de cargas individuales (ver arriba).
La curva de momento asociada es entonces un polígono.
En las esquinas del polígono los resultados coinciden con los resultados exactos,
que están dados por un recorrido cuadrado en el área de la línea de carga, corresponden exactamente.
El curso de la fuerza cortante asociada adquiere entonces forma escalonada (discontinuo).
En el medio de cada intervalo de paso hay acuerdo con el curso exacto continuo.
Existe otro programa para calcular los esfuerzos internos en estructuras estáticamente indeterminadas: Estructuras Estaticamente Indeterminadas.
otras aplicaciones en JavaScript