Schnittgrößen bei statisch bestimmten Rahmentragwerken
Es werden hier Auflagerreaktionen sowie der Verlauf von Biegemoment, Querkraft und Normalkraft für statisch bestimmte Biegebalken (Durchlaufträger) und unverzweigte Strukturen berechnet.
Zu den Eingabedaten
Das Programm kennt nur Einzellasten.
Will man eine konstante Streckenlast q0 näherungsweise darstellen, benötigt man in einem belasteten Bereich der Länge L mehrere Punkte.
Bei n äquidistanten Punkten (n einschließlich Anfangs- und Endpunkt) erhalten die inneren Punkte eine Last der Größe q0·L/(n-1) und die beiden Randpunkte jeweils die Hälfte davon.
Allgemeine Beobachtungen
Bei geraden Balken sind die Verläufe der 3 Schnittgrößen stetig bis auf Stellen, wo zugehörige Lasten/Lagerreaktionen angreifen.
An solchen Lasteinleitungsstellen entstehen jeweils Sprünge entsprechend der Größe der eingeleiteten Last.
Der Normalkraftverlauf und der Querkraftverlauf sind bereichsweise konstant.
Der Biegemomentenverlauf ist bereichsweise linear veränderlich.
Bei Strukturen mit unterschiedlich ausgerichteten Teilbereichen haben der Querkraftverlauf und der Normalkraftverlauf Sprünge an den Ecken der Struktur.
Der Momentenverlauf an den Ecken ist jedoch in der Regel stetig.
Sprünge entstehen nur, wenn an einer Ecke ein Moment eingeleitet wird.
Zu den Ergebnissen
Nur wenn ein horizontaler Balken untersucht wird, wird im Diagramm als Ordinate die jeweilige Schnittgröße aufgetragen.
Die Vorzeichen der Schnittgrößen richten sich hier nach einem lokalen xyz-Koordinatensystem,
dessen x-Achse nach rechts und dessen z-Achse nach unten zeigt. Die y-Achse zeigt aus der Darstellungsebene heraus.
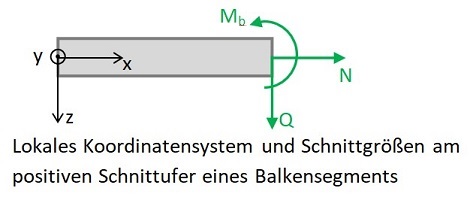
Ein Biegemoment am rechten Ende eines Balkensegments (positives Schnittufer) ist positiv,
wenn es rechts um die aus der Darstellungsebene heraus zeigende y-Achse wirkt.
Eine Querkraft ist am rechten Ende eines Balkensegments positiv, wenn sie nach unten wirkt.
Bei Rahmentragwerken orientieren sich die Vorzeichen am lokalen xyz-Koordinatensystem des jeweiligen Rahmensegmentes.
Die lokale x-Achse zeigt vom ersten zum zweiten Punkt des Segments. Die lokale z-Achse zeigt, wenn man entlang der lokalen x-Achse blickt, nach rechts.
Ein Biegemoment ist somit am zweiten Punkt des Segments positiv, wenn es links rum wirkt.
Längskräfte sind hinsichtlich der Vorzeichen am einfachsten zu diskutieren:
Positive Normalkräfte stehen für eine Zugbelastung, negative Normalkräfte stehen für eine Druckbelastung.
Das Programm kennt zwar keine Streckenlasten.
Konstante Streckenlasten lassen sich allerdings relativ gut durch eine Gruppe von Einzellasten abbilden (s.o.).
Der zugehörige Momentenverlauf ist dann ein Polygonzug.
An den Ecken des Polygonzuges stimmen die Ergebnisse mit den exakten Ergebnissen,
die ja durch einen quadratischen Verlauf im Bereich der Streckenlast gegeben sind, exakt überein.
Der zugehörige Querkraftverlauf ist dann treppenförmig (unstetig).
In der Mitte jedes Stufenintervalls besteht Übereinstimmung mit dem stetigen exakten Verlauf.
Für die Berechnung der Schnittgrößen bei statisch unbestimmten Tragwerken gibt es ein anderes Programm: 2D-Rahmentragwerke.
weitere JavaScript-Programme