Efforts internes dans Structures isostatiques
Ici, les réactions d'appui ainsi que la courbe du moment fléchissant, de l'effort tranchant et de l'effort normal sont calculées pour des poutres de flexion déterminées statiquement (poutres continues) et des structures non ramifiées.
Vers les données d'entrée
Le programme ne connaît que les charges individuelles.
Si vous souhaitez représenter une charge linéaire constante q0 approximativement, vous avez besoin de plusieurs points dans une zone chargée de longueur L.
Pour n points équidistants (n incluant les points de début et de fin), les points intérieurs reçoivent une charge de taille q0·L/(n-1) et les deux bords en pointe chaque moitié.
Observations générales
Dans le cas de poutres droites, les courbes des trois efforts internes sont continues jusqu'aux points où les charges/réactions d'appui associées prennent effet.
À ces points d'introduction de charge, des sauts se produisent en fonction de la taille de la charge introduite.
En supposant l'existence uniquement de charges ponctuelles, les propriétés suivantes s'appliquent:
- La courbe de force normale et la courbe de force de cisaillement sont constantes dans certaines zones.
- La courbe du moment de flexion est variable linéairement dans certaines zones.
Dans les structures avec des zones partielles alignées différemment, la courbe de force de cisaillement et la courbe de force normale présentent des sauts aux coins de la structure.
Cependant, la courbe du moment de flexion aux coins est généralement continue.
Les sauts ne se produisent que lorsqu'un moment est introduit dans un coin.
Vers les résultats
Ce n'est que si une barre horizontale est examinée que la force interne correspondante est tracée dans le diagramme sous forme d'ordonnée.
Les signes des efforts internes sont basés sur un système de coordonnées local xyz,
dont l'axe x pointe vers la droite et dont l'axe z pointe vers le bas. L'axe Y pointe hors du plan d'affichage.
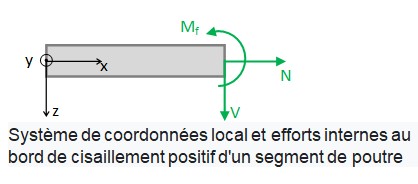
Un moment de flexion à l'extrémité droite d'un segment de poutre (banc à coupe positive) est positif,
s'il agit vers la droite autour de l'axe y pointant vers le plan de représentation.
Une force de cisaillement est positive à l'extrémité droite d'un segment de poutre si elle agit vers le bas.
Pour les structures de cadre, les signes sont basés sur le système de coordonnées local xyz du segment de cadre respectif.
L'axe des x local pointe du premier au deuxième point du segment. L'axe z local pointe alors vers la droite dans la direction de visualisation de cet axe x local.
Un moment fléchissant est donc positif à l'extrémité d'un segment respectif s'il agit vers la gauche.
Les forces longitudinales sont plus faciles à discuter en termes de signes:
Les forces normales positives représentent une charge de traction, les forces normales négatives représentent une charge de compression.
Le programme ne connaît aucune charge de ligne.
Les charges linéaires constantes peuvent cependant être relativement bien représentées par un groupe de charges individuelles (voir ci-dessus).
La courbe de moment associée est alors un polygone.
Aux coins du polygone, les résultats concordent avec les résultats exacts,
qui sont donnés par un tracé carré dans la zone de charge linéaire, correspondent exactement.
La progression de l'effort tranchant associée est alors en forme d'étape.
Au milieu de chaque intervalle de pas, il y a un accord avec le parcours exact continu.
Il existe un autre programme pour calculer les efforts internes dans les structures statiquement indéterminées: Structures statiquement indéterminées.
Plus de logiciels en JavaScript
